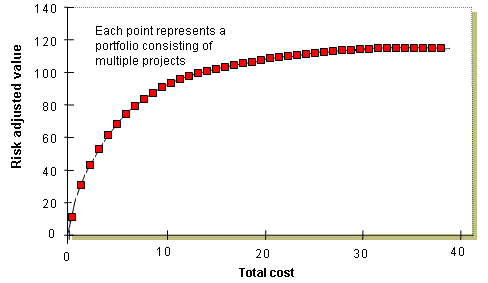
L’obiettivo per quanto riguarda la costruzione di un portafoglio progetti è di selezionare insiemi di progetti in grado di creare il maggior valore in rapporto ai rischi connessi senza superare i vincoli sulle risorse disponibili.
A tal fine il valore atteso deve essere messo in rapporto al valore a rischio introducendo il concetto di “risk adjusted”.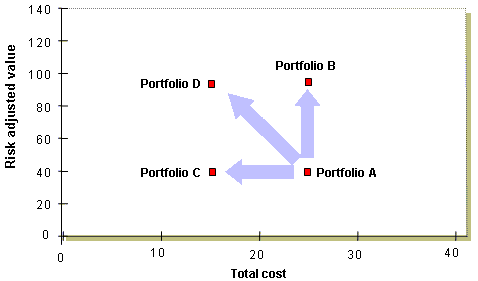
Nella teoria economica, l’insieme di investimenti che crea il maggior valore risk adjusted al minor costo viene chiamato frontiera efficiente. Questo approccio viene in particolare seguito nella valutazione dell’asset allocation finanziaria e può essere applicato con profitto nell’analisi del portafoglio progetti.
Molte organizzazioni hanno difficoltà ad individuare il giusto mix di progetti su cui concentrare gli investimenti e di conseguenza non riescono ad ottimizzare il processo di creazione di valore.
Ciò corrisponde all’incapacità di determinare la frontiera efficiente.
Mentre da un lato è relativamente semplice calcolare il valore di un portafoglio di progetti se si seguono le giuste metriche, dall’altro non è altrettanto semplice individuare la giusta combinazione di portafogli e progetti che massimizza il valore complessivamente generato al costo minore.
E’ proprio a tal fine che la determinazione della frontiera efficiente viene in aiuto.
Supponiamo che un’organizzazione posizioni su un grafico come quello riportato nella figura a lato i vari portafogli progetti alternativi in base al costo ed al valore creato corretto in base al rischio (risk adjusted).
La teoria economica definisce il portafoglio A come inefficiente, perché c’è un altro portafoglio di progetti, il portafoglio B, che produce più valore per lo stesso costo.
Analogamente, vi è anche un portafoglio C che produce lo stesso valore per un costo minore. Inoltre, vi è un portafoglio D con una combinazione di queste due caratteristiche.
Supponiamo ora di considerare tutti i portafogli di progetti alternativi che possono essere costruiti a partire da una serie di progetti candidati. Tipicamente ce ne sono moltissimi. 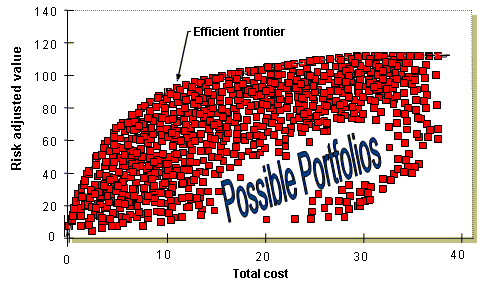
Nel caso riportato a lato, l’organizzazione aveva 30 proposte di progetto in esame in un unico ciclo di definizione del budget. Quattro di questi progetti sono stati ritenuti obbligatori, lasciando 26 progetti discrezionali.
In generale, se ci sono N progetti potenziali, ci sono 2N possibili portafogli di progetti. (Questo accade perché ci sono un totale di 2N sottoinsiemi all’interno di un insieme di N elementi).
Ciò porta alla necessità di valutare 226 portafogli che comporta un numero molto elevato di iterazioni rendendo necessario l’utilizzo di un software apposito oppure di motori di calcolo sempre più presenti all’interno dei tools di project portfolio management.
Obiettivo di queste elaborazioni è l’individuazione dei portafogli che si distribuiscono lungo la frontiera efficiente.
Come si può vedere ogni portfolio che contribuisce a definire la curva si caratterizza in base al valore creato ed al costo.
La curva stessa presenta da un certo punto in poi un andamento piatto che sconsiglia di prendere in considerazione quei portafogli che oltrepassano una certa soglia.
In tal caso può essere utile applicare l’analisi di Pareto ponendo il punto di selezione all’80% in modo da identificare quel portafoglio composto da quel 20% di progetti candidati che permette di conseguire l’80% del valore potenzialmente conseguibile in base alla frontiera efficiente (regola 80/20).
Solitamente la frontiera efficiente migliora se si aumentano le opzioni disponibili a livello di progetto (ad esempio con 3 versioni alternative per lo stesso progetto) e analoghi miglioramenti si ottengono nel tempo attraverso il progressivo affinamento delle modalità di analisi da parte di un’organizzazione che utilizza ripetutamente tale strumento per definire le proprie scelte di portafoglio.